Bienvenidos a mi blog en esta entrada aquí entenderás un concepto sobre la tabla de verdad, o tabla de valores de verdad, es una tabla que muestra el valor de verdad de una proposición compuesta, para cada combinación de verdad que se pueda asignar.1
Fue desarrollada por Charles Sanders Peirce por los años 1880, pero el formato más popular es el que introdujo Ludwig Wittgenstein en su Tractatus logico-philosophicus, publicado en 1921.
Para establecer un Sistema formal se establecen las definiciones de los operadores. Las definiciones se harán en función del fin que se pretenda al construir el sistema que haga posible la formalización de argumentos:
- Como razonamientos deductivos lógico-lingüísticos
- Como construcción de un sistema matemático puro
- Como una aplicación lógica en un Circuito de conmutación.
Verdadero
 |  |  |
El valor verdadero se representa con la letra V; si se emplea notación numérica se expresa con un uno: 1; en un circuito eléctrico, el circuito está cerrado.
Falso
 |  |  |
El valor falso se representa con la letra F; si se emplea notación numérica se expresa con un cero: 0; en un circuito eléctrico, el circuito está abierto.
Variable
 | 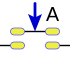 |  |
Para una variable lógica A, B, C, ... pueden ser verdaderas V, o falsas F, los operadores fundamentales se definen así:
Negación
 |  |  |
La negación operador que se ejecuta, sobre un único valor de verdad, devolviendo el valor contradictorio de la proposición considerada.
Conjunción
 |  | 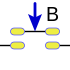 |  |
La conjunción es un operador, que actúa sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando ambas proposiciones son verdaderas, y falso en cualquier otro caso. Es decir, es verdadera cuando ambas son verdaderas.
En términos mas simples, será verdadera cuando las dos proposiciones son verdaderas.
La tabla de verdad de la conjunción es la siguiente:
Que se corresponde con la columna 8 del algoritmo fundamental.
en simbología "^" hace referencia a el conector "y"
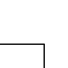
Disyunción
 |  |  |  |
 |  |  |  |
La disyunción es un operador lógico que actúa sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando una de las proposiciones es verdadera, o cuando ambas lo son, y falso cuando ambas son falsas.
En términos mas simples, será verdadera cuando por lo menos una de las proposiciones es verdadera de lo contrario será falsa.
La tabla de verdad de la disyunción es la siguiente:
Que se corresponde con la columna 2 del algoritmo fundamental.
Implicación o Condicional
 |  |  |  |
 |  |  |  |
El condicional material es un operador que actúa sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de falso sólo cuando la primera proposición es verdadera y la segunda falsa, y verdadero en cualquier otro caso.
La tabla de verdad del condicional material es la siguiente:
Que se corresponde con la columna 5 del algoritmo fundamental.
Equivalencia, doble implicación o Bicondicional
 |  |  |  |
 |  |  |  |
El bicondicional o doble implicación es un operador que funciona dando el valor de verdad cuando ambos valores son iguales y dando el valor de falsedad cuando ambos valores son diferentes.
La tabla de verdad del bicondicional es la siguiente:
Que se corresponde con la columna 7 del algoritmo fundamental.
EN EL SIGUIENTE VÍDEO PODRÁN VER DE UNA FORMA SIMPLE Y SENCILLA LA TABLA DE VERDAD
FORMULAS LOGICAS EQUIVALENTES
Definición:
Dos fórmulas lógicas son equivalentes si tienen los mismos valores de verdad para todos los posibles valores de verdad de sus componentes atómicos.
Diremos que dos proposiciones P y Q son lógicamente equivalentes si es una tautología, es decir, si las tablas de verdad de P y Q son iguales.
Leyes Lógicas
- Asociativas
- Distributivas
- Leyes de De Morgan
- De idempotencia
- De identidad
- De dominación
- Inversas
- De absorción
Reglas de Sustitución
- Sea P una tautología y q una variable de P. Si sustituimos cada aparición de q por cualquier otra proposición Q entonces la proposición resultante es también una tautología.
- Sea P una tautología y Q una proposición que aparece en P. Si reemplazamos Q por una proposición lógicamente a Q obtendremos una nueva proposición lógicamente equivalente a P.
- Cualquier proposición es lógicamente equivalente a otra que contiene sólamente los conectivos lógicos -, v,and.
Reglas de Inferencia
Dadas dos proposiciones P y Q diremos que P implica lógicamente Q , y escribiremos P \Rightarrow Q si P rightarrow Q es una tautología.
Si P es falso, entonces la proposición P, Q es verdadera independientemente del valor de Q. Por tanto, P si los valores de las variables que hacen a P verdadero también hacen verdadero a Q. De manera equivalente P Q significa que P y Q no tienen nunca de manera simultánea los valores de verdad 1 y 0 respectivamente.
Como hemos dicho, las proposiciones pueden tomar dos valores, verdadero o falso, que representaremos respectivamente con los números 1 y 0. Por tanto, cuando digamos que una proposición toma valor 1 estaremos diciendo que es verdadera.
El valor de verdad de una proposición compuesta queda determinado por los valores de las proposiciones simples que la forman. Las tablas de verdad nos indican los valores de verdad de una proposición para cada posible combinación de los valores de las proposiciones simples.
Equivalencia lógica en la ley asociativa de la conjunción
A modo ilustrativo demostraremos, a continuación, que, en virtud de la ley asociativa de la conjunción, la fórmula p(qr) es lógicamente equivalente a (pq)r.
Para ello no hay más que hacer la tabla de verdad de cada una de esas expresiones y comprobar si, en efecto, todas sus interpretaciones son iguales para la conectiva dominante.
Equivalencia lógica en la ley asociativa de la disyunción
Te proponemos que rellenes la siguiente tabla con “Vs” y “Fs” donde proceda para comprobar que, en virtud de la ley asociativa de la disyunción, la fórmula p(qr) es equivalente a (pq)r.
Ejemplo: Las dos fórmulas siguientes son equivalentes:
(p → ¬q) ∨ (¬p ∨ r) ¬p ∨ ¬q ∨ r
| p | q | r | ¬q | ¬p | p → ¬q | ¬p ∨ r | (p → ¬q) ∨ (¬p ∨ r) | ¬ p ∨ ¬q | ¬p ∨ ¬q ∨ r |
| V | V | V | F | F | F | V | V | F | V |
| V | V | F | F | F | F | F | F | F | F |
| V | F | V | V | F | V | V | V | V | V |
| V | F | F | V | F | V | F | V | V | V |
| F | V | V | F | V | V | V | V | V | V |
| F | V | F | F | V | V | V | V | V | V |
| F | F | V | V | V | V | V | V | V | V |
| F | F | F | V | V | V | V | V | V | V |
donde se puede observar que la última y la antepenúltima columnas son iguales.
Las equivalencias se relacionan con las tautologías de la siguiente forma.
AQUÍ PODRÁN VER UN VÍDEO EXPLICÁNDOLO MAS DETALLADAMENTE


“Una proposición sólo es idéntica consigo misma”.

“Una proposición no puede ser verdadera y falsa a la vez”.

“Una proposición o es verdadera o es falsa, no hay una tercera opción”.

“La negación de la negación es una afirmación”.


“Las variables repetidas redundantemente en una cadena de conjunciones o en una cadena de
disyunciones se reemplazan por la sola variable”.



“En una proposición, la conjunción, la disyunción inclusiva y la bicondicional son conmutativas”.



“En una proposición, la doble conjunción, la doble disyunción, o la doble bicondicional se asocian
indistintamente”.




“En una proposición la conjunción, la disyunción y la implicación son distributivas”.


“En una proposición, la negación de una conjunción o de una disyunción son distributivas
respecto a la disyunción o conjunción.


“En una proposición, la condicional equivale a la disyunción de la negación del antecedente con el consecuente, y la negación de una condicional equivale a una conjunción del antecedente con la
negación del consecuente”.










![Rendered by QuickLaTeX.com [(p \Rightarrow q) \wedge p] \Rightarrow q](https://soloformulas.com/wp-content/ql-cache/quicklatex.com-b715b50f580152687ca2006c22432eba_l3.png)
“En una premisa condicional; si se afirma el antecedente, entonces se concluye en la afirmación
del consecuente”.
![Rendered by QuickLaTeX.com [(p \Rightarrow q) \wedge ~ p] \Rightarrow ~ p](https://soloformulas.com/wp-content/ql-cache/quicklatex.com-971eae00cf98e0d9486ce8a2d89a7545_l3.png)
“En una proposición, si se niega el consecuente de una premisa condicional entonces se concluye
en la negación del antecedente”.
![Rendered by QuickLaTeX.com [(p \vee q) \wedge ~ p] \Rightarrow q](https://soloformulas.com/wp-content/ql-cache/quicklatex.com-53071b440bdc7c99652ec79f556f4f20_l3.png)
“En una proposición, cuando se niega el antecedente de la premisa de una disyunción, se concluye en la afirmación del consecuente”.
![Rendered by QuickLaTeX.com [(p \Leftrightarrow q) \wedge p] \Rightarrow q](https://soloformulas.com/wp-content/ql-cache/quicklatex.com-547b53ca64dcfeda018e9aca9340584c_l3.png)
“En una proposición, cuando se afirma que uno de los miembros de una bicondicional es verdadera,
entonces el otro miembro también es verdadero”.
![Rendered by QuickLaTeX.com [(p \Rightarrow q) \wedge (q \Rightarrow s)] \Rightarrow (p \Rightarrow s)](https://soloformulas.com/wp-content/ql-cache/quicklatex.com-7d376b7569215fb743eaadc6510140ea_l3.png)
“En una proposición, el condicional es transitivo”.
![Rendered by QuickLaTeX.com [(p \Leftrightarrow q) \wedge (q \Leftrightarrow s)] \Rightarrow (p \Leftrightarrow s)](https://soloformulas.com/wp-content/ql-cache/quicklatex.com-b7da3d04c3db6b0cc1c7e06e55ff1dda_l3.png)
“En una proposición, el bicondicional es transitivo”.

“En una proposición, si el antecedente y consecuente de una conjunción son verdades, entonces
cualquiera de los dos términos es verdad”.
DE ADICIÓN:

“En una proposición, una disyunción está implicada por cualquiera de sus dos miembros.
 La puerta lógica O, más conocida por su nombre en inglés OR (), realiza la operación de suma lógica.
La puerta lógica O, más conocida por su nombre en inglés OR (), realiza la operación de suma lógica.
 La puerta lógica OR-exclusiva, más conocida por su nombre en inglés XOR, realiza la función booleana A'B+AB'. Su símbolo es (signo más "+" inscrito en un círculo). En la figura de la derecha pueden observarse sus símbolos en electrónica.
La puerta lógica OR-exclusiva, más conocida por su nombre en inglés XOR, realiza la función booleana A'B+AB'. Su símbolo es (signo más "+" inscrito en un círculo). En la figura de la derecha pueden observarse sus símbolos en electrónica.
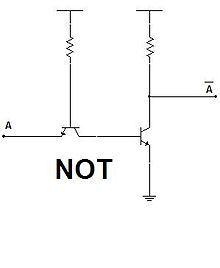
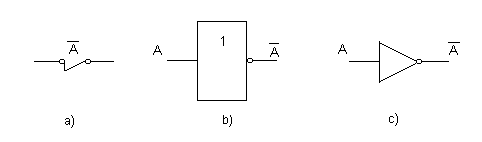 La puerta lógica NO (NOT en inglés) realiza la función booleana de inversión o negación de una variable lógica. Una variable lógica (A) a la cual se le aplica la negación se pronuncia como "no A" o "A negada".
La puerta lógica NO (NOT en inglés) realiza la función booleana de inversión o negación de una variable lógica. Una variable lógica (A) a la cual se le aplica la negación se pronuncia como "no A" o "A negada".
El álgebra booleana es usada para expresar la relación entre entradas y salidas de circuitos lógicos. Las constantes y variables solo pueden tener dos valores posibles: 0 y 1.
CONSTANTE Y VARIABLE.-
En álgebra booleana no hay fracciones, decimales,números negativos, raíz cuadrada, raíz cúbica,logaritmos, números imaginarios…
operación NOT se realiza con una sola variable.
El mapa de Karnaugh es una herramienta muy útil para la simplificación y minimización de expresiones algebraicas Booleanas. Es similar a una tabla de verdad, ya que muestra todos los posibles valores de las variables de entrada y la salida resultante para cada valor.
AQUÍ PODRÁN VER UN VÍDEO EXPLICÁNDOLO MAS DETALLADAMENTE
LEYES LÓGICAS PRINCIPALES
DE IDENTIDAD:
“Una proposición sólo es idéntica consigo misma”.
DE CONTRADICCIÓN:
“Una proposición no puede ser verdadera y falsa a la vez”.
DEL TERCIO EXCLUÍDO:
“Una proposición o es verdadera o es falsa, no hay una tercera opción”.
DE LA DOBLE NEGACIÒN O INVOLUCIÓN:
“La negación de la negación es una afirmación”.
DE LA IDEMPOTENCIA:
“Las variables repetidas redundantemente en una cadena de conjunciones o en una cadena de
disyunciones se reemplazan por la sola variable”.
DE LA CONMUTATIVIDAD:
“En una proposición, la conjunción, la disyunción inclusiva y la bicondicional son conmutativas”.
DE LA ASOCIATIVIDAD:
“En una proposición, la doble conjunción, la doble disyunción, o la doble bicondicional se asocian
indistintamente”.
DE LA DISTRIBUTIVIDAD:
“En una proposición la conjunción, la disyunción y la implicación son distributivas”.
DE MORGAN:
“En una proposición, la negación de una conjunción o de una disyunción son distributivas
respecto a la disyunción o conjunción.
DEL CONDICIONAL:
“En una proposición, la condicional equivale a la disyunción de la negación del antecedente con el consecuente, y la negación de una condicional equivale a una conjunción del antecedente con la
negación del consecuente”.
DEL BICONDICIONAL:
DE LA ABSORCIÓN:
DE TRANSPOSICIÓN:
DE EXPORTACIÓN:
MODUS PONENS:
“En una premisa condicional; si se afirma el antecedente, entonces se concluye en la afirmación
del consecuente”.
MODUS TOLLENS:
“En una proposición, si se niega el consecuente de una premisa condicional entonces se concluye
en la negación del antecedente”.
DEL SILOGISMO DISYUNTIVO:
“En una proposición, cuando se niega el antecedente de la premisa de una disyunción, se concluye en la afirmación del consecuente”.
DE LA INFERENCIA EQUIVALENTE:
“En una proposición, cuando se afirma que uno de los miembros de una bicondicional es verdadera,
entonces el otro miembro también es verdadero”.
DEL SILOGISMO HIPOTÉTICO:
“En una proposición, el condicional es transitivo”.
DE LA TRANSITIVIDAD SIMÉTRICA:
“En una proposición, el bicondicional es transitivo”.
DE LA SIMPLIFICACIÓN:
“En una proposición, si el antecedente y consecuente de una conjunción son verdades, entonces
cualquiera de los dos términos es verdad”.
DE ADICIÓN:
“En una proposición, una disyunción está implicada por cualquiera de sus dos miembros.
SIMPLIFICACIÓN DE FORMULAS PROPOSICIONALES
VÍDEO EXPLICATIVO
CIRCUITOS LÓGICOS
¿QUE ES UN CIRCUITO LÓGICO?
Los circuitos lógicos por lo general sirven únicamente como una ayuda auxiliar necesaria para lograr un mejor entendimiento de los caracteres simbólicos no gráficos.
LOGICA DE BITS(not,and,or,xor)
Puerta AND
La puerta lógica Y, más conocida por su nombre en inglés AND (), realiza la función booleana de producto lógico. Su símbolo es un punto (·), aunque se suele omitir. Así, el producto lógico de las variables A y B se indica como AB, y se lee A y B o simplemente A por B.
La ecuación característica que describe el comportamiento de la puerta AND es:
Su tabla de verdad es la siguiente:
| Entrada | Entrada | Salida |
|---|---|---|
Así, desde el punto de vista de la aritmética módulo 2, la compuerta AND implementa el producto módulo 2.
Puerta OR
La ecuación característica que describe el comportamiento de la puerta OR es:
Su tabla de verdad es la siguiente:
| Entrada | Entrada | Salida |
|---|---|---|
Podemos definir la puerta OR como aquella que proporciona a su salida un 1 lógico si al menos una de sus entradas está a 1.
Puerta OR-exclusiva (XOR)
La ecuación característica que describe el comportamiento de la puerta XOR es:
Su tabla de verdad es la siguiente:
| Entrada | Entrada | Salida |
|---|---|---|
Se puede definir esta puerta como aquella que da por resultado uno, cuando los valores en las entradas son distintos. ej: 1 y 0, 0 y 1 (en una compuerta de dos entradas). Se obtiene cuando ambas entradas tienen distinto valor.
Si la puerta tuviese tres o más entradas, la XOR tomaría la función de suma de paridad, cuenta el número de unos a la entrada y si son un número impar, pone un 1 a la salida, para que el número de unos pase a ser par. Esto es así porque la operación XOR es asociativa, para tres entradas escribiríamos: a(bc) o bien (ab)c. Su tabla de verdad sería:
| Entrada | Entrada | Entrada | Salida |
|---|---|---|---|
Desde el punto de vista de la aritmética módulo 2, la puerta XOR implementa la suma módulo 2, pero mucho más simple de ver, la salida tendrá un 1 siempre que el número de entradas a 1 sea impar.
Lógica negada
Puerta NO (NOT)
La ecuación característica que describe el comportamiento de la puerta NOT es:
Su tabla de verdad es la siguiente:
| Entrada | Salida |
|---|---|
Se puede definir como una puerta que proporciona el estado inverso del que esté en su entrada.
COMPUERTAS LOGICAS Y ALGEBRA DE BOOLE
El álgebra booleana es usada para expresar la relación entre entradas y salidas de circuitos lógicos. Las constantes y variables solo pueden tener dos valores posibles: 0 y 1.
En
ciertos sistemas digitales,
0 booleano = cualquier voltaje entre 0 y 0.8 volts.
1 booleano = cualquier voltaje entre 2 y 5 volts.
0 y
1 booleano no representan números, si no el estado de una variable de
voltaje. Llamado nivel lógico
Otras
términos usados sinónimos de 0 y 1.
CONSTANTE Y VARIABLE.-
En álgebra booleana no hay fracciones, decimales,números negativos, raíz cuadrada, raíz cúbica,logaritmos, números imaginarios…
Solo tres operaciones básicas
(operaciones lógicas):OR, AND y NOT.
Los
circuitos digitales que realizan operaciones lógicas son llamados circuitos lógicos.
PUERTA OR
La operación OR produce un resultado (salida) de 1 cuando cualquier entrada sea 1. Si no, la salida es 0.
La
expresión booleana es:
PUERTA AND
La
salida es 1 lógico solo si todas las entradas son 1.
Caso contrario la
salida es 0.
La
expresión booleana es:
PUERTA NOT
operación NOT se realiza con una sola variable.
Su salida es presentada como:
MAPAS KARNAUGH
El mapa de Karnaugh es una herramienta muy útil para la simplificación y minimización de expresiones algebraicas Booleanas. Es similar a una tabla de verdad, ya que muestra todos los posibles valores de las variables de entrada y la salida resultante para cada valor.
Es una secuencia de celdas en la que cada celda representa un valor binario de las variables de entrada. El número de celdas de un mapa de Karnaugh es igual al número total de combinaciones de las variables de entrada, al igual que el número de filas para una tabla de verdad, es decir, si un mapa tiene 3 variables, (2) elevado a la 3 = 8.
Las celdas del mapa K se marcan de modo que las celdas horizontalmente y verticalmente adyacentes, solo difieran en una variable.
Vamos a definir algunos términos que nos son de mucha utilidad al momento de analizar los mapas K:
Implicante: Un grupo de unos ó ceros adyacentes que implican a una variable en cuestión, agrupados en potencias de a dos.
Adyacencia: Característica de un mapa K en el que sólo se cambia una variable de una celda a otra inmediata a ella por cualquiera de sus cuatro lados
Mapa de Karnaugh de dos variables
El mapa de Karnaugh de dos variables es un conjunto de cuatro celdas.
La siguiente figura nos muestra la tabla de verdad y el mapa K para una función escogida arbitrariamente de dos variables.
| La función definida por la tabla en minterms es: | ||||